My HP laptop's HDD had been giving some errors in the Disk test for quite sometime now, so I got a new HDD with the idea to clone the old disk on this new disk. And to connect this new HDD to computer I bought a USB based 2.5 HDD External interface for HDDs, which allows you to connect the laptop disk to your system through usb cable.
My primary reason to go for cloning the disk was I wanted to avoid starting with a fresh image of Windows and the job of installing the dozens of softwares all over again. Plus I had Ubuntu installation in one of the partitions. This seemed like a perfect use-case for disk cloning.
So, a bit of google search on disk cloning landed me on this page: https://en.wikipedia.org/wiki/Comparison_of_disk_cloning_software
I tried a couple of softwares from the above list. To keep it easy I started off with the Windows based softwares:
My primary reason to go for cloning the disk was I wanted to avoid starting with a fresh image of Windows and the job of installing the dozens of softwares all over again. Plus I had Ubuntu installation in one of the partitions. This seemed like a perfect use-case for disk cloning.
So, a bit of google search on disk cloning landed me on this page: https://en.wikipedia.org/wiki/Comparison_of_disk_cloning_software
I tried a couple of softwares from the above list. To keep it easy I started off with the Windows based softwares:
- Acronis True Image[1] This one is a paid software, but luckily the new HDD I got was WD, and it turned out that if you have a WD HDD on your system, the software doesn't ask for the license and you get to use it for free. But this one turned out to be a a disappointing one as it failed to recognize my HDD as WD drive (probably because I was interfacing it through USB).
- Macrium Reflect This was my next bet, as its a freeware with Graphical interface so going for easy one again :P. Was easy to install and then followed the GUI wizard to clone the disk, and bingo the cloning began. However as luck would have it, a couple of hours later the dialog box saying "Disk read error" popped out of no where and I was back to square one !
I realized that windows was not up to the task, the easy route was turning out to be rather difficult now.
So, I rebooted into Ubuntu this time to try the REAL low level stuff.
- dd - is what I started with in Linux. You can create disk backups and disk cloning with a single line of this command (see thats the power of linux ;). To clone 'sda' to 'sdb' you can use the command (use at your own risk):
dd if=/dev/sda of=/dev/sdb bs=4096 conv=notrunc,noerror
ps -ef | grep 'dd' # get the PID of dd command
kill -USR1 8789 #senda signal to 'dd' process to print the progress- WARNING: If you are thinking of trying this, please read this link, and understand what exactly you are doing because a small mistake can make you lose all your data. https://wiki.archlinux.org/index.php/Disk_Cloning
- It turned out 'dd' is just a simple copying command with no error handling built into it, so couple of hours into copying this one too failed with "input/output error" on the console :-/
- Then i tried to manually create partitions on the new disk using fdisk.
sudo fdisk -l #shows the disks and partition details for all disks
sudo fdisk /dev/sdc # if you need to partition '/dev/sdc'
- The above command takes you to the fdisk command prompt, where you can easily 'create new partition', 'delete a partition' and 'write your changes to partition table' etc. However, this was turing out to be cumbersome process, because I would have to clone all partitions one by one and format them using mkfs and what not :P http://www.idevelopment.info/data/Unix/Linux/LINUX_PartitioningandFormattingSecondHardDrive_ext3.shtml
- Now comes the real awesome piece of software to my rescue - 'ddrescue'. Yeah as the name says, so it does :). This is similar to 'dd' but has disk error handling algorithm built into it. What it tries to do is recover as much of the data from the disk as is possible from the good sectors, and then uses slow reading to recover the bad sectors. You can find all the details here: http://www.gnu.org/software/ddrescue/manual/ddrescue_manual.html
sudo ddrescue -f /dev/sda /dev/sdb logfile- 'ddrescue' has an awesome log feature which basically logs all the disk recovery it is doing to a file. This log file allows it to resume the recovery process from where it left, incase your system crashes in between or anything !!
- You can also get a 'ddrescueview' which shows the graphical view of the recovery process as good/bad sectors etc. which is really helpful. You can download this from here: http://sourceforge.net/projects/ddrescueview/
To summarize, yeah 'ddrescue' was able to clone my old disk to the new one. And the log viewer GUI showed that my old disk had one (just one :P) bad sector in my Windows partition. But yeah, overall this turned out to be a great learning experience about disks ;)
![\Pr[a\le X\le b] = \int_a^b f(x) \, dx](http://upload.wikimedia.org/math/d/7/1/d715cf83d8a655fdfc1d3a90433cd62c.png)



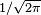 in this expression ensures that the total area under the curve ϕ(x) is equal to one
in this expression ensures that the total area under the curve ϕ(x) is equal to one ; and has
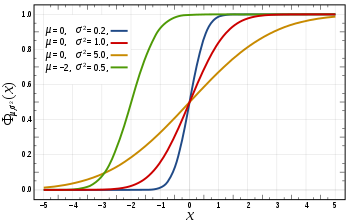
; and has ![[-\infty, x]](http://upload.wikimedia.org/math/f/e/a/fea1695aef424e4676dafd2ddad0445d.png) , as a function of x. The CDF of the standard normal distribution, usually denoted with the capital Greek letter
, as a function of x. The CDF of the standard normal distribution, usually denoted with the capital Greek letter 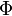 (
(