Another Good read:
http://highlyscalable.wordpress.com/2012/05/01/probabilistic-structures-web-analytics-data-mining/
Original Post: http://lkozma.net/blog/sketching-data-structures/#comment-85892
“Sketching” data structures store a summary of a data set in situations where the whole data would be prohibitively costly to store (at least in a fast-access place like the memory as opposed to the hard disk). Variants of trees, hash tables, etc. are not sketching structures, they just facilitate access to the data, but they still store the data itself. However, the concept of hashing is closely related to most sketching ideas as we will see.
The main feature of sketching data structures is that they can answer certain questions about the data extremely efficiently, at the price of the occasional error. The best part is that the probability of an error can be quantified and the programmer can trade off the expected error rate with the amount of resources (storage, time) afforded. At the limit of this trade-off (when no error is allowed) these sketching structures collapse into traditional data structures.
Sketching data structures are somewhat counter-intuitive, but they can be useful in many real applications. I look at two such structures mostly for my own benefit: As I try to understand them, I write down my notes. Perhaps someone else will find them useful. Links to further information can be found in the end. Leave comments if you know of other sketching data structures that you found useful or if you have some favorite elegant and unusual data structure.
1. Bloom filter
Suppose we have to store a set of values (A) that come from a “universe” of possible values (U). Examples: IP addresses, words, names of people, etc. Then we need to check whether a new item xis a member of set A or not. For example, we might check if a word is spelled correctly by looking it up in the dictionary, or we can verify whether an IP address is banned by looking it up in our black list.
We could achieve this by storing the whole set A in our favorite data structure. Alternatively, we could just store a binary array, with one bit for each possible element in U. For example, to quickly check if a number is prime or not, we could precompute an array of bits for all numbers from 0 to the maximum value we need:
Prime = 001101010001010001010001...
To check whether a number is prime, we look at the corresponding bit and we are done. This is a dummy example, but it is already obvious that in most cases the range of possible values is too large to make this practical. The number of all possible strings of length 5, containing just letters from the English alphabet is 26^5 = 11,881,376 and in most real problems the universe U is much larger than that.
The magic of the Bloom filter allows us to get away with much less storage at the price of an occasional mistake. This mistake can only be a false positive, the Bloom filter might say that x is in A when in fact it is not. On the other hand, when it says that x is not in A, this is always true, in other words false negatives are impossible. In some applications (like the spell-checker), this is acceptable if false positives are not too frequent. In other applications (like the IP blacklist), misses are more common and in the case of a hit, we can verify the answer by reading the actual data from the more costly storage. In this case the Bloom filter can act as an efficiency layer in front of a more costly storage structure. If false positives can be tolerated, the Bloom filter can be used by itself.
The way it works is really simple: we use a binary array of size n, as in the prime numbers example, that is initialized with 0s. In this case however, n is much smaller than the total number of elements in U. For each element to be added to A, we compute k different hash values (using k independent hash functions) with results between 1 and n. We set all these locations h1, h2, …, hk (the indexes returned by the hash functions) in the binary array to 1. To check if y is in A, we compute the hash values h1(y), …, hk(y) and check the corresponding locations in the array. If at least one of them is 0, the element is missing. If all fields are 1, we can say that the element is present with a certainty that depends on n (the size of the array), k (the number of hashes) and the number of elements inserted. Note that n and k can be set beforehand by the programmer.
The source of this uncertainty is that hash values can collide. This becomes more of a problem as the array is filling up. If the array were full, the answer to all queries would be a yes. In this simple variant, deleting an element is not possible: we cannot just set the corresponding fields to 0, as this might interfere with other elements that were stored. There are many variants of Bloom filters, some allowing deletion and some allowing the storage of a few bits of data as well. For these and for some rigorous analysis, as well as some implementation tricks, see the links below.
A quick dummy example is a name database. Suppose we want to store female names and reject male names. We use two hash functions that return a number from 1 to 10 for any string.
Initial configuration: 0000000000
Insert("Sally") : 0100000001
# h1("Sally") = 2, h2("Sally") = 10
Insert("Jane") : 1110000001
# h1("Jane") = 1, h2("Jane") = 3
Insert("Mary") : 1110100001
# h1("Mary") = 5, h2("Mary") = 2 [collision]
Query("Sally")
# bits 2 and 10 are set,
# return HIT
Query("John")
# h1("John") = 10 set, but h2("John") = 4 not set
# return MISS
Query("Bob")
# h1("Bob") = 5 set, h2("Bob") = 1 set
# return HIT (false positive)
2. Count-Min sketch
The Count-Min (CM) sketch is less known than the Bloom filter, but it is somewhat similar (especially to the counting variants of the Bloom filter). The problem here is to store a numerical value associated with each element, say the number of occurrences of the element in a stream (for example when counting accesses from different IP addresses to a server). Surprisingly, this can be done using less space than the number of elements, with the trade-off that the result can be slightly off sometimes, but mostly on the small values. Again, the parameters of the data structure can be chosen such as to obtain a desired accuracy.
CM works as follows: we have k different hash functions and kdifferent tables which are indexed by the outputs of these functions (note that the Bloom filter can be implemented in this way as well). The fields in the tables are now integer values. Initially we have all fields set to 0 (all unseen elements have count 0). When we increase the count of an element, we increment all the corresponding k fields in the different tables (given by the hash values of the element). If a decrease operation is allowed (which makes things more difficult), we similarly subtract a value from all k elements.
To obtain the count of an element, we take the minimum of the kfields that correspond to that element (as given by the hashes). This makes intuitive sense. Out of the k values, probably some have been incremented on other elements also (if there were collisions on the hash values). However, if not all k fields have been returned by the hash functions on other elements, the minimum will give the correct value. See illustration for an example on counting hits from IP addresses:
In this example the scenario could be that we want to notice if an IP address is responsible for a lot of traffic (to further investigate if there is a problem or some kind of attack). The CM structure allows us to do this without storing a record for each address. When we increment the fields corresponding to an address, simultaneously we check if the minimum is above some threshold and we do some costly operation if it is (which might be a false alert). On the other hand, the real count can never be larger than the reported number, so if the minimum is a small number, we don’t have to do anything (this holds for the presented simple variant that does not allow decreases). As the example shows, CM sketch is most useful for detecting “heavy hitters” in a stream.
It is interesting to note that if we take the CM data structure and make the counters such that they saturate at 1, we obtain the Bloom filter.
For further study, analysis of the data structure and variants, proper choice of parameters, see the following links:
What is your favorite counter-intuitive data structure or algorithm?
![\Pr[a\le X\le b] = \int_a^b f(x) \, dx](http://upload.wikimedia.org/math/d/7/1/d715cf83d8a655fdfc1d3a90433cd62c.png)
in this expression ensures that the total area under the curve Ï•(x) is equal to one
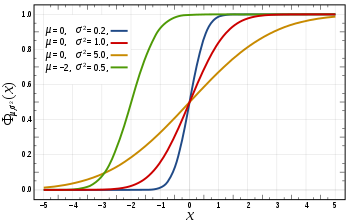
; and has ![[-\infty, x]](http://upload.wikimedia.org/math/f/e/a/fea1695aef424e4676dafd2ddad0445d.png)
, as a function of x. The CDF of the standard normal distribution, usually denoted with the capital Greek letter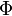 
(
